Jackbox Chalices

This is a fun little math problem that pops out of a game called Trivia Murder Party. This game functions as a pretty straightforward trivia game, covering a variety of topics, from questions I know to questions I don't know. When a player gets a question wrong, they have to play a mini game to not get eliminated. One of these games is Chalices. This game has a specific survival rate based on the number of players, and it yields a surprising (at least to me) result.

The chalices game is very simple. There are some cups lined cup across the bottom of the screen, with various design. The players that did not get the question wrong each choose a cup to poison, following which the player that got the previous question wrong selects a cup. If they pick a safe cup, they survive. If they pick a poisoned cup, they are eliminated. That's it! Think of the holy grail in Indiana Jones and the Last Crusade.

There are a few small but important mathematical considerations: First, the players poisoning the cups cannot communicate or coordinate with each other; Second, while the various cup designs certainly add a bit of psychological warfare (the skull cup for example is a bit on the nose), we will assume players pick randomly; Lastly, while multiple players can fail—changing the number of poisoned cups—we will assume only one player failed that question. Interestingly, this assumption doesn’t affect the result when we take the limit later. Before diving into the math, take a moment to guess: do you think your chances of survival improve or worsen as more players join?

The question is simply, given a certain number of players, what is the chance that you will survive?

In short, the math comes out to the following formula, where $n=\text{number of cups}$.

$$\frac{\text{Success}}{\text{Total}}=\frac{(n-1{)}^{n-1}}{n^{n-1}}$$

Since this is a party game, it's natural to wonder whether your survival odds improve or worsen as more players join. Since the number of cups is growing, you have more to choose from. However, this means more poisoners as well. It's clear that if the poisoners coordinate your odds will get increasingly worse ($1/n$), but they do not.

On one hand, as the number of cups increases, it seems like the chances of picking a safe one should approach zero—after all, there are more players ($n-1$ poisoners) and more poisoned cups. However, since players cannot coordinate, multiple poisoners may choose the same cup, reducing the overall number of poisoned cups. Since there are more poisioners, it's also increasingly likely they will overlap. Because of these competing factors, it's not obvious (at least to me) whether your survival chances improve or worsen as the game scales.

Based on these two competing forces, it's hard to see if your odds get better or worse. We have the formula for this, so we can easily plot it and check our intuition.

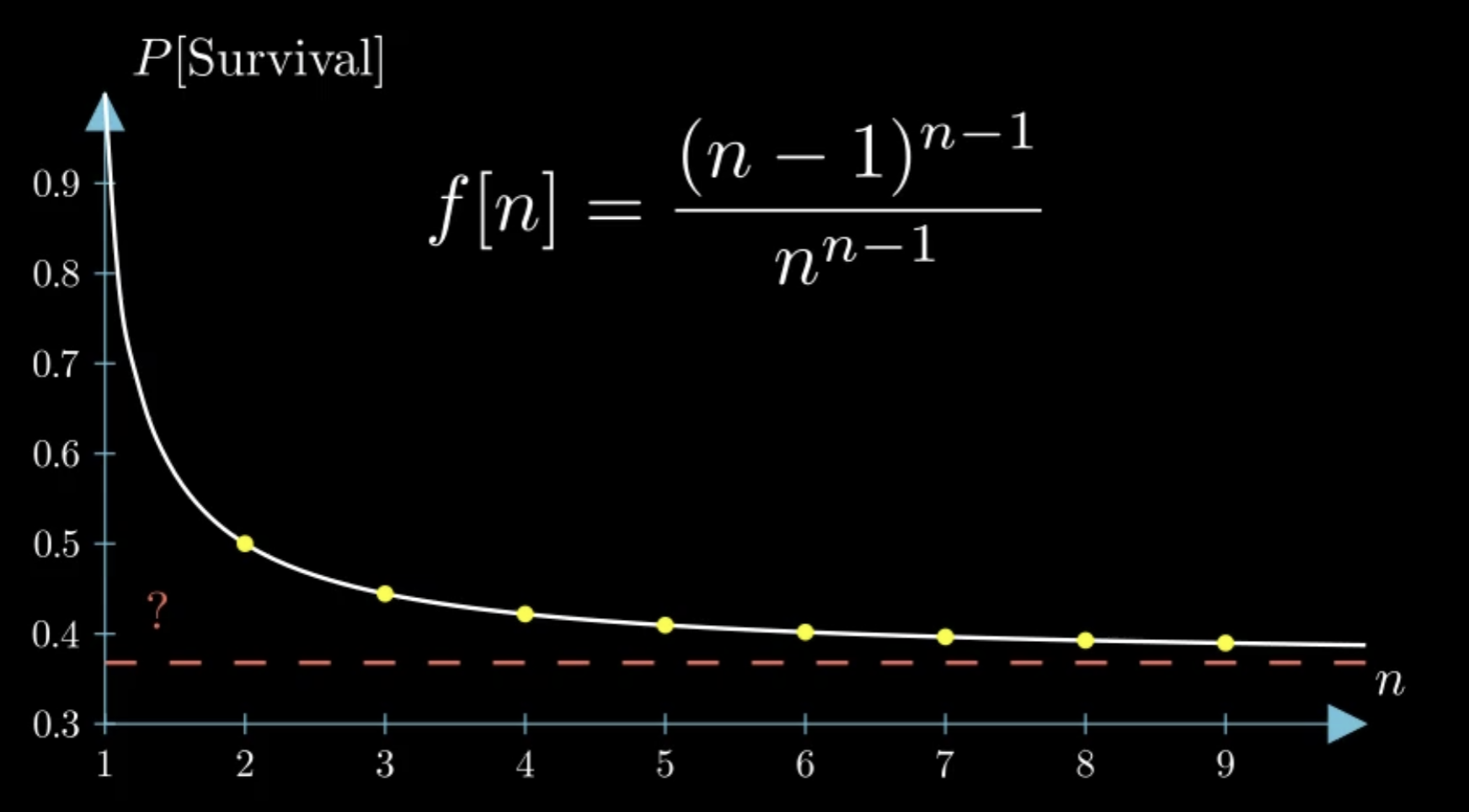
As expected, we have 50% for 2 people, around 44% for 3 players, and increasingly worse odds as the number of players increases. It seems to approach a specific value! It turns out those competing forces tend to "cancel" to a constant probability. The question becomes what is this value.

Taking this limit, we find a value of $1/e\approx 0.368$ appears. Much like the Secretary Problem we have this $1/e$ value pop out of the derivation.

From a game design standpoint, this is really nice because it means that the game is never too hard or too easy (unless you're playing trivia with 2/3 people, which is unlikely considering this is a Jackbox Party Pack). Makes me wonder if it was intentional; at the very least, I'm going to pretend like it was.